I had an interview for a project the other day. The challenge was to conjure a vending machine algorithm. Its main computational problem seems to be the coin-purse management. Consider a very simple loop that given a pound sterling amount in pence -all future examples will also use amounts in pence- finds all the combinations of coins to make it up.
void BruteForce(int total)
{
if (total<=0) return; // Just a sanity check.
for (int p200 = 0; p200 <= total / 200; p200++)
{ // 200p loop
int total200 = total - p200 * 200;
for (int p100 = 0; p100 <= total200 / 100; p100++)
{ // 100p loop
int total100 = total200 - p100 * 100;
for (int p50 = 0; p50 <= total100 / 50; p50++)
{ // 50p loop
int total50 = total100 - p50 * 50;
for (int p20 = 0; p20 <= total50 / 20; p20++)
{ // 20p loop
int total20 = total50 - p20 * 20;
for (int p10 = 0; p10 <= total20 / 10; p10++)
{ // 10p loop
int total10 = total20 - p10 * 10;
for (int p5 = 0; p5 <= total10 / 5; p5++)
{ // 5p loop
int total5 = total10 - p5 * 5;
for (int p2 = 0; p2 <= total5 / 2; p2++)
{ // 2p loop
int total2 = total5 - p2 * 2;
for (int p1 = 0; p1 <= total2; p1++)
{ // 1p loop
int total1 = total2 - p1;
if (
200 * p200
+ 100 * p100
+ 50 * p50
+ 20 * p20
+ 10 * p10
+ 5 * p5
+ 2 * p2
+ p1 == total); // Gotcha!
}
}
}
}
}
}
}
}
}The loop is not optimized. It simply iterates through all possible coin combinations given target amount in p. Nedless to say, the Gotcha! comment in this and all future code samples marks the spot where the solution has been found...but we don't do anything with it.Well, actually, it is slightly optimized. For example if the requested amount is 5p all outer loops (for coins of larger denomination) will only execute once.The following two graphs show the total number of loops executed for totals up to £5 (500p) and the number of solutions found.
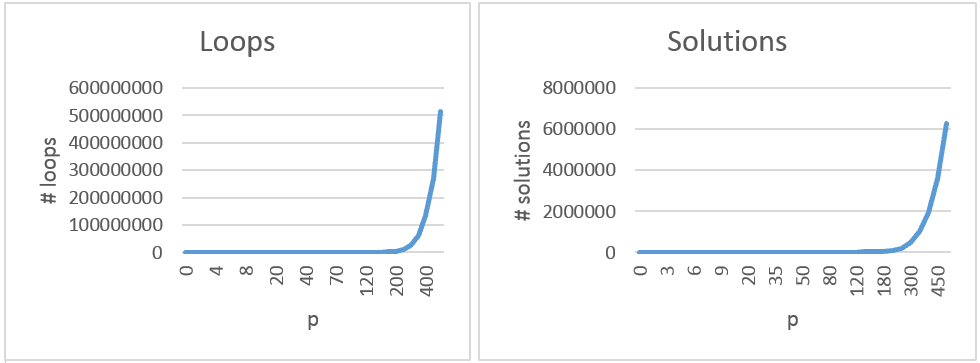
Number of required computations grows exponentionally. And though CPU power is cheap these days, and possibility of vending machine returning more then £5 is minimal - it makes sense to optimize it. Let’s write the same code using recursion.
void RecursiveBruteForce(int coin, int total)
{
if (coin == 0) return; // Exit criteria.
else
for (int qty = total / coin; qty >= 0; qty--)
if (coin * qty == total); // Gotcha!
else RecursiveBruteForce(coin==50?20:coin/2, total-coin*qty);
}That is easier to the eye, but just as greedy. Oh, yes. That coin==50?20:coin/2 is an optimization for finding first smaller coin then current coin from an aging 8-bit assembler programmer ( that would be me :) ). Could be refactored into GetNextCoin(int coin) function to have cleaner, albeit slower code. We transformed loops into a recursive tree search.Now let’s optimize it a bit more by considering the stock of available coins already in the purse. After all we can’t return coins we don’t have. To do this we will assume existence of function int AvailableQty(int coin). No rocket science here:
void RecursiveAvailQty(int coin, int total)
{
if (coin == 0) return; // Exit criteria.
else
for (int qty = Math.Min(AvailableCoins(coin), total / coin); qty >= 0; qty--)
if (coin * qty == total); // Gotcha!
else RecursiveAvailQty (coin==50?20:coin/2, total-coin*qty);
}Since our client does not want tens of coins returned another idea for optimization is to minimize the quantity of coins returned and cut all search tree branches that exceed this.The recursion chooses coins with largest nomination first. This by itself is heuristics and already optimizes the number of coins by directing the search. But there are occasions where this approach does not work. For example: if the vending machine has a supply of 1 x 50p, 3 x 20p, and 10 x 1p and wants to return 60p. By using largest nomination first the first solution will be 1 x 50p, 10 x 1p (11 coins). But wouldn’t you as a client feel much better if the machine returned 3 x 20p (3 coins)?Following code shows algorithm, returning minimal number of coins.
void RecursiveCoinMinimizing(int coin, int total, ref int minqty, int totalqty)
{
if (coin == 0) return; // Exit criteria.
else
for (int qty = Math.Min(AvailableCoins(coin), total / coin); qty >= 0; qty--)
if (coin * qty == total) minqty=Math.Min(minqty, totalqty + qty); // Gotcha!
else if (totalqty + qty < minqty)
RecursiveCoinMinimizing(coin==50?20:coin/2, total-coin*qty, ref minqty, totalqty+qty);
}
To summarize our optimizations:- Our heuristics starts with coins with largest denomination first.
- It cuts all imposible tree branches (that would require quantities of coins we don’t have).
- It then minimizes the quantity coins returned to the client.
- And cuts all tree branches that would contain larger quantity of coins then the solution that we have already found.
Because we start with coins with largest denomination, gradually reducing the quantity of coins with large denomination will increase the total quantity of coins in potential solutions and increase the possibility for the branch to be cut early.
Here is the Coin Minmizing Algorithm at work.
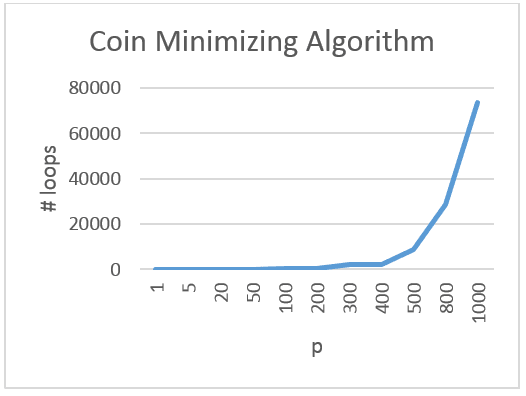
Given unlimited coins in the purse the initial brute force algorithm without any optimization would need to loop 513.269.189 times to find all possible combinations for paying out £5. The Coin Minimizing Algorithm would need to loop only 8.774 times. Even returning £10 can be achieved in real time on an average embedded hardware. If we limit inserting of coins to max. £10 then this solution is considered relatively safe.
So let us call it a day here. :) Sure – there are other optimizations possible. But 1) vending machines are not developed in an evening; these are serious revenue generating softwares and they need serious attention, and 2) this is illustrative enough to shows the approach taken.
Besides speed further optimizations could also include strategies for example defensive behaviour by the vending machine to theoretically minimize the number of failed transactions. This could, perhaps, be done by asset allocation (assigning each denumeration a % of total quantity). And then making rare coins –according to asset allocation- more “expensive” thus directing the search and computing utility value of each generated solution.
Categories algorithms , c# , elegant
Subscribe to:
Post Comments
(
Atom
)
0 comment(s) :
Post a Comment