W I S C H N E R

Sometimes you want a function to return an object or null if no object is found. Lazy evaluation makes it easy to automate this behaviour.

public Person FindPerson(Criteria c)
{
    Lazy<Person> person = new Lazy<Person>();
    // Code to actually find a person ...
    // ... and populate person.Value
    return person.IsValueCreated ? person.Value : null;
}

This is fairly ellegant. If no person is found lazy evaluation assures that the object is never created and related resources are not spent. Be careful though! Here's a common pest.

foreach (Font font in GetFixedFonts())
{
    // But GetFixedFonts returned null.
}

The fictional GetFixedFonts() function called in code bellow returns Font[] collection. You assume it will always return a non- null value. But then on a bad day it doesn't and your code breaks with an exception.

You can assure that function always returns an array /even if empty/ by using lazy evaluation too. Here is an example of that.

public FontFamily[] GetFixedFonts()
{
    Lazy<List<FontFamily>> fonts = new Lazy<List<FontFamily>>();

    foreach (FontFamily ff in System.Drawing.FontFamily.Families)
        if (IsFixedFontFamily(ff))
            fonts.Value.Add(ff);

    return fonts.Value.ToArray();
}

You know the drill. Programming a graph takes too much time...use a library...or hire an external consultant. But...is it really so?

Imagine you have two coordinate systems. Your physical screen coordinate system spans from 0 to window's width horizontally and from 0 to window's height vertically. And your imaginary world (i.e. a map) spans from -10.000 to 10.000 horizontally and from 0 to 5000 vertically.

Just to make things a bit more complex you also want to:
- zoom everything on the screen by arbitrary zoom factor, and
- show only part of your map on the screen starting from point T(-3.000, 1000) given in map coordinates, where -3000 is left and 1000 is top coordinate of part of map we would like to display on screen.

Map to Screen

Are you scared yet? Don’t be. Here is the basic formula for converting map coordinate to screen coordinate:

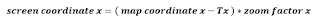
Same formula can be applied to another dimension. For example:

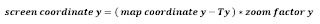
So far ... so trivial. :) Since you start at point T(x,y) you need to put x and y to point to 0,0 on the screen. Afterwards you simply multiply by zoom factor. If factor is 1 then 1 point on the map is converted to 1 point on the screen. If the factor is 1:2 then 1 point on the map is only ½ point on the screen. And so on.

If the axis is a reverse axis then your equation is:

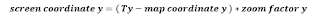
Screen to Map

What if somebody clicks on the screen and we need to find map coordinate of the click? Let us derive this scenario from the above equation:

Deriving same formula for the reverse axis is a good exercise for you, don’t you agree? :)

Fit to Screen

If we want to fit our map inside the screen we must start drawing it at its T=T0 point. We calculate T by using:

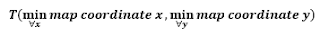
No big secrets here. So our left, right point T is at map's min x and min y. And if reverse axis is being used we must use max instead.

The apropriate fit to screen zoom is calculated like this:

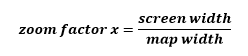
If you are using same unit for both axes then there will be only one zoom factor. To still fit map to the screen make sure that you fit larger dimension of both - width or height to fit the screen. Then use the same zoom factor for smaller dimension. This way both are guaranteed to fit the screen.

Calculate Distances

Last but not least ... distances are calculated with a little help from previous calculations. If you have a distance in screen units and you would like to convert to map distance you subtract it from point zero and derive the formula like this:

The distance obviously depends on the zoom factor alone. For better understanding derive the opposite formula and get screen distance from map distance yourself. :)

Coming Next...

So there you have it. Most of these formulas are -in fact- just simplified 4 x 4 matrix translation, usually performed for you by modern 2D graphics engines such as GDI+ or Cairo.

Observing simplicity of graph math one realizes that graphs aren't really such a terrible development effort. It's drawing points, lines and polygons using these formulas to translate coordinates. Zooming is changing the zoom factor, and scrolling is changing the T point. We will take a closer look at these operations in part two of this series.

A singleton is like the Egg of Columbus. Easy after someone had showed you how to do it. Luckily Jon Skeet had showed us how to use lazy evaluation for thread safety. And an unknown contributor of Great Maps had demonstrated the usage of generics for that purpose. So all that is left for me - is to put it all together.

public sealed class Singleton<T> where T : new()
{
    private static readonly Lazy<T> instance = new Lazy<T>(() => new T());

    public static T Instance { get { return instance.Value; } }

    private Singleton()
    {
    }
}

// Create two server objects pointing to the same instance.
Server svr1 = Singleton<Server>.Instance;
Server svr2 = Singleton<Server>.Instance;

Reference:
- C# In Depth: Implementing the Singleton Pattern in C#
- GMap.NET Singleton Class